Voronoi Diagram and Delaunay Triangulation

Diagram voronoi adalah salah satu cabang ilmu yang dipelajari dalam perkuliahan geometri komputasi yang muncul pada abad ke 17. Diagram voronoi pertama kali di pikirkan oleh René Descartes  pada tahun 1644 dan digunakan oleh Dirichlet pada tahun 1850. Kemudian Voronoi pada tahun 1907 mengembangkannya ke dalam dimesi yang lebih tinggi. Walaupun demikian, Voronoi dan Dirichlet adalah orang yang pertama kali memperkenalkan konsep Diagram voronoi secara formal. Mereka menerapkan konsep tersebut dalam kajian bentuk kuadrat. Hasil dari studi tersebut kemudian disebut Dirichlet tessellation atau Voronoi diagram. Salah satu penggunaan Diagram voronoi yang paling spektakuler adalah analisis penyakit kolera di London pada tahun 1854, dimana fisikawan John Snow menemukan hubungan yang kuat anatara kematian dengan penggunaan air pompa yang terinfeksi di Broad Street.

 Gambar1. Diagram voronoi

Secara matematis, Diagram voronoi di definisikan sebagai berikut:

Misal P adalah himpunan n (jarak titik-titik dalam sebuah bidang). Diagram voronoi dari P adalah pembagian bidang tersebut dalam n sel (bagian), satu untuk setiap titik.Titik q terletak pada sel (bagian) yang sesuai dengan titik  p_i element of P. Persamaan matematisnya adalah

Batas dari dua daerah voronoi dismbolkan V(S) dan disebut voronoi edge (rusuk voronoi), jika terdiri lebih dari satu titik. Titik sudut dari rusuk voronoi disebut Voronoi vertices (sudut voronoi); yang dibatasi oleh tiga atau lebih daerah voronoi.

Gambar 2. Diagram voronoi untuk 11 titik pada bidang Euclid.

Dengan mengajarkan siswa tentang Diagram voronoi, mereka akan dapat mengembangkan kemampuan spatial reasoning mereka. Hal ini dapat dilakukan dengan menggunakan pendekatan matematika realistik, yaitu dengan memulai memberikan soal atau masalah konteks bagi siswa. Misalnya ada lima kantor pos yang ada di wilayah kota Palembang. Bagaimana caranya gar pelanggan atau masyarakat mengetahui kantor pos mana yang paling dekat didaerah mereka? Pertanyaan ini dapat diselesaikan dengan menggunakan konsep atau pengetahuan tentang Diagram voronoi.

The Delaunay Triangulation adalah triangulasi yang setara dengan saraf dari sel-sel dalam diagram Voronoi, yaitu, bahwa triangulasi convex hull dari titik-titik dalam diagram di mana setiap circumcircle segitiga adalah lingkaran kosong (Okabe et al. 1992, hal. 94).

 

Hubunngan dengan diagram voronoi

 

The Delaunay Triangulation with all the circumcircles and their centers (in red).

 

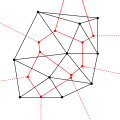
Connecting the centers of the circumcircles produces the Voronoi diagram (in red).

Sumber :
https://bustangbuhari.wordpress.com/2011/10/10/voronoi-diagram-sebuah-pengantar/
http://mathworld.wolfram.com/VoronoiDiagram.html
http://mathworld.wolfram.com/DelaunayTriangulation.html
https://en.wikipedia.org/wiki/Voronoi_diagram
https://en.wikipedia.org/wiki/Delaunay_triangulation